Ballistic Quantum Transport in Nanoscale Transistors: a Non Equilibrium Green’s Function Approach
Introduction
As MOS field-effect transistors are scaled down to a nanometer regime, quantum effects in both transverse and transport directions start playing a major role in determining device characteristics. In order to address a new challenge, SILVACO has started a deployment of new quantum mechanical models based on Non Equilibrium Green’s Function (NEGF) approach. This is a fully quantum mechanical approach which treats such effects as source-to-drain tunneling, ballistic transport, and quantum confinement on equal footing. The new NEGF solver is suitable to model ballistic quantum transport in such devices as Double Gate or Surround Gate MOSFET, using rectangular or cylindrical geometries in ATLAS. The method used is based on references [1] and [2].
Simulations
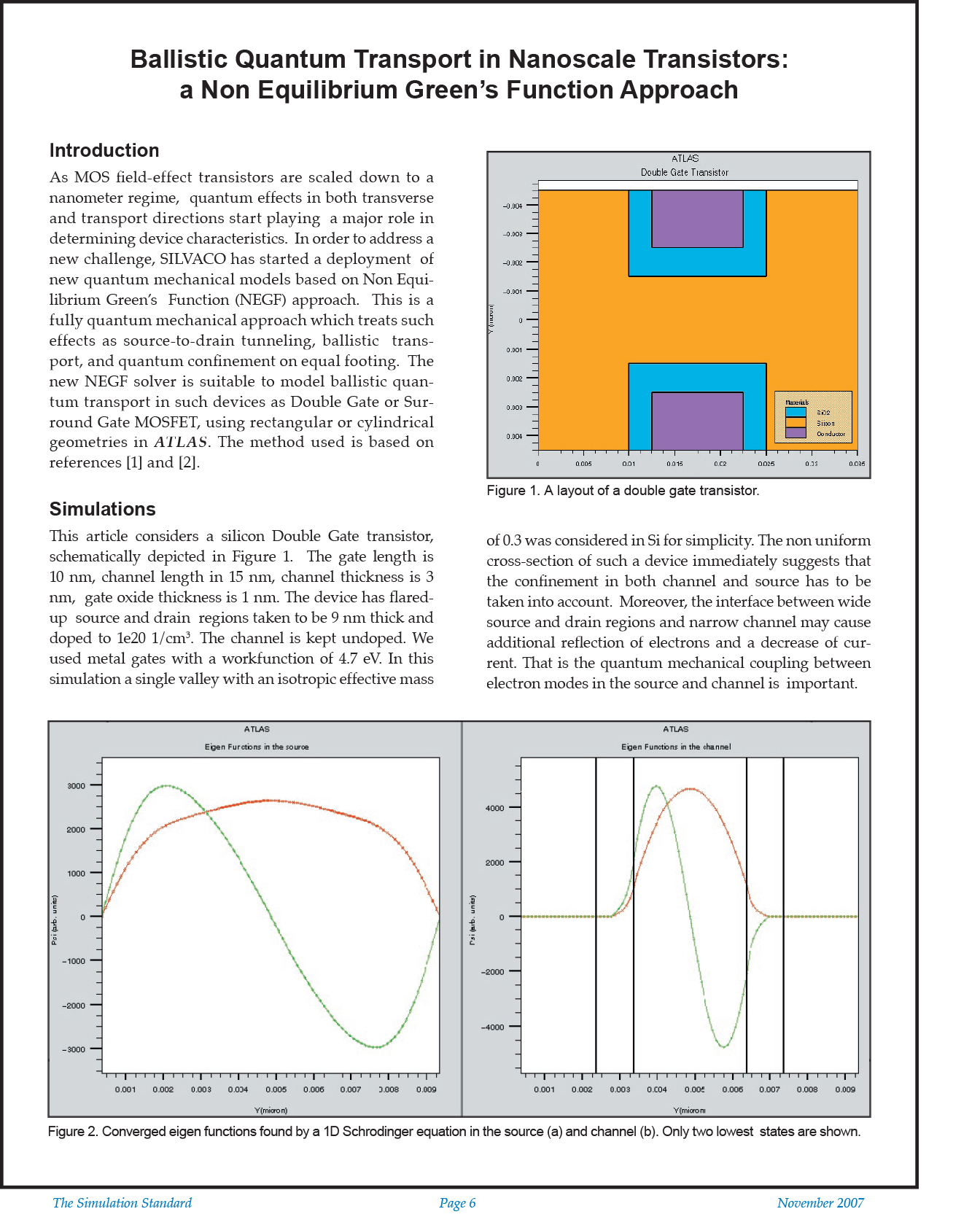
This article considers a silicon Double Gate transistor, schematically depicted in Figure 1. The gate length is 10 nm, channel length in 15 nm, channel thickness is 3 nm, gate oxide thickness is 1 nm. The device has flared-up source and drain regions taken to be 9 nm thick and doped to 1e20 1/cm3. The channel is kept undoped. We used metal gates with a workfunction of 4.7 eV. In this simulation a single valley with an isotropic effective mass of 0.3 was considered in Si for simplicity. The non uniform cross-section of such a device immediately suggests that the confinement in both channel and source has to be taken into account. Moreover, the interface between wide source and drain regions and narrow channel may cause additional reflection of electrons and a decrease of current. That is the quantum mechanical coupling between electron modes in the source and channel is important.
The modeling starts with a solution of 1D Schrodinger equation in the transverse slices of the device in order to find eigen functions and eigen energies, shown in Figure 2 and 3 respectively. Note that the penetration of electrons into oxide is accurately taken into account. ATLAS will automatically decide on the number of required eigen states in each slice, as this number changes from source to drain and is different for different biases. If desired, the number of eigen states may be set manually.